The Nspire non-CAS can use the Numerical Solver (nsolve) to find numerical solutions,
and you can also Graph to find numerical solutions.
When working graphically, you will, in most cases, have to adjust
your windows to see the graphs.
(on this page, rounding to nearest hundredth will be occurring where needed)
(nsolve) Examples:
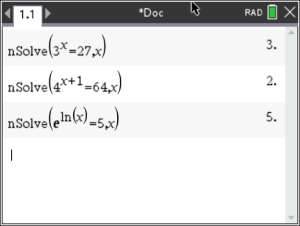
1. Solve for x: 3x = 27.
(start with one where we know the answer)
Answer:
x = 3
2. Solve for x: 4x+1 = 64.
Answer: x = 2
3. Solve for x: e ln(x) = 5
Answer: x = 5
Steps:
• Start on a "Calculator" page.
•  . #3 Algebra, #1 Numerical Solution
• Enter equation: nSolve(3x = 27, x). 
|
|
Graphical Examples: (Solve for the variable.)
1. 
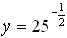
This is a simple calculation problem.
Enter the right hand side of the equation on a "calculator" page to perform the calculation.
Let's see what the calculator will
do.
Enter just the right hand side of the equation on the calculator screen to
perform the calculation.
Answer:
y = .2 or 1/5
Actually, you can find this answer by hand very easily by using properties of exponents. |
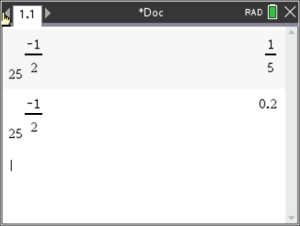
To change fraction to decimal hit CTRL, ENTER. |
2.
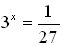
Enter the left side into f1
and the right side into f2.
Keep in mind that 1/27 is a very small value.
Adjust your
window accordingly until you see clearly what is happening with the graphs.
Then use your intersect option.
, 6, 4 Intersection
Answer: x = -3 |
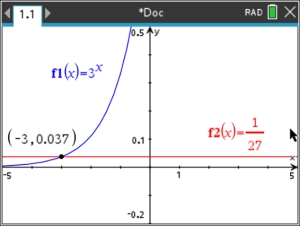 Window: x: -5 to 5, increment 1
y: -0.2 to 0.5, increment 0.1 |
3.
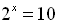
Proceed as in #2.
Adjust the window to see the intersection.
Answer: x = 3.32 |
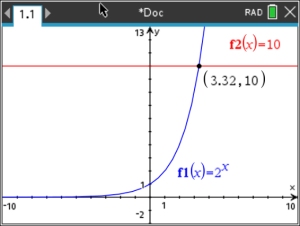 Window: x: -10 to 10, increment 1
y: -2 to 13, increment 1 |
4. 
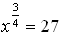
Proceed as in #2. Be sure to adjust the window to allow
for a y-value of 27. Also notice the need to move to the
right to find the intersection.
Increase the XMax value.
Answer: x = 81
Did you notice that this graph is not an "exponential" function. It is a "power" function, since x is in the base. |
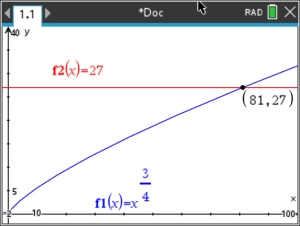 Window: x: -2 to 100, increment 10
y: -2 to 40, increment 5 |
5.
Solve this system:
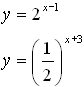
Enter both functions. Use the intersect option.
The standard window should suffice in this problem. Or adjust as you see fit to get a clear picture of what is happening.
Answer: x = -1, y
= 0.25 |
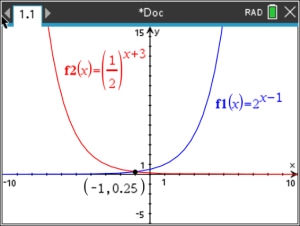 Window: x: -10 to 10, increment 1
y: -5 to 15, increment 1 |
6. Solve for
x, to the nearest tenth:
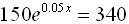
Proceed as in #2. Adjust the window as to see the point of
intersection of the two functions.
Answer: x = 16.4 |
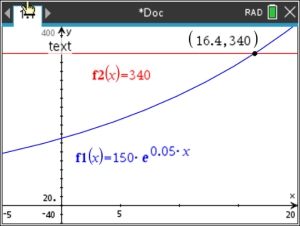 Window: x: -5 to 20, increment 5
y: -40 to 400, increment 20 |
|
